颗粒分布

MFIX-Exa 可以生成 constant （单分散或单一尺寸）的颗粒，或遵循 normal 、 log-normal 或 uniform 分布的多分散颗粒。用户可以通过提供离散概率文本输入文件来指定自定义 custom 分布。

除了分布类型之外，还必须指定 分布权重 ；MFIX-Exa 支持两种分布权重：

数目加权直径分布

数目加权直径密度函数 \(f_X^N(x)\,dx\) 可以解释为定义直径在 \(x\) 和 \(x+dx\) 之间的 颗粒数量，除以颗粒总数。

体积加权直径分布

体积加权直径密度函数 \(f_X^V(x)\,dx\) 同样可以解释为定义直径在 \(x\) 和 \(x+dx\) 之间的 颗粒体积，除以颗粒总体积。

警告

数目加权和体积加权分布不可互换。未能指定正确的分布权重可能导致意外行为。

代码使用两种分布权重，计算（或近似）未提供的分布权重。例如，如果提供了数目加权正态分布， 则计算相应的体积加权正态分布。体积加权分布用于计算在初始条件区域中生成的颗粒（或包裹）的数量。 在创建 DEM 颗粒时*采样*数目加权分布，而在创建 PIC 包裹时*采样*体积加权分布。 对 PIC 包裹采样体积加权分布允许用较少的包裹表示非常小的颗粒，而用更多的包裹表示分布中的大颗粒。 包裹的统计权重经过调整，以便准确表示数量分布。

以下部分概述了 MFIX-Exa 支持的分布及其行为控制的输入参数。

constant 分布

constant 分布定义了单分散（单值）分布，并使用以下输入：

	描述	类型	默认值
constant	单分散分布的大小	实数	N/A

在以下示例中，一个长方体被填充了直径为 1 mm、密度为 2500 kg·m^-3 的单分散颗粒。初始条件区域体积为 0.001 m³，固体体积分数为 0.05（5% 固体）。

列表 10 定义 constant 分布的输入片段。这不是完整的输入文件。

# 定义 IC 和 BC 的区域
# -----------------------------------------------------------------------
mfix.regions = full-domain

regions.full-domain.lo  = 0.0  0.0  0.0
regions.full-domain.hi  = 0.1  0.1  0.1

# 初始条件
# -----------------------------------------------------------------------
ic.regions = full-domain

mfix.particle_init_type = Auto

# 全域
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~>
ic.full-domain.fluid.volfrac  = 0.95

ic.full-domain.fluid.density  = 1.0
ic.full-domain.fluid.pressure = 0.0
ic.full-domain.fluid.velocity = 0.0  0.0  0.0

ic.full-domain.solids  = solid0

ic.full-domain.packing = random

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = constant
ic.full-domain.solid0.diameter.constant = 1000.e-6  # (m)

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  = 2500.0    # (kg/m^3)

一个 MFIX-Exa DEM 模拟生成大约 95,500 个颗粒，而在 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 64 和欧拉网格间距 \(\Delta x\) 为 3.125 mm 的情况下，PIC 模拟生成大约 164,000 个包裹。

normal 分布

normal 或高斯分布由以下公式给出

(1)\[f_X(x) = \frac{d}{dx}F_X(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp{\left(- \frac{(x - \mu)^2 }{ 2 \sigma^2 }\right)}\]

其中参数 \(\mu\) 是分布的均值，\(\sigma\) 是标准差。用于指定分布的输入参数如下表所示。

	描述	类型	默认值
type	分布权重： number-weighted 或 volume-weighted	字符串	N/A
mean	正态随机变量的均值，\(X\)	实数	N/A
std	正态随机变量的标准差，\(X\)	实数	N/A
min	最小粒径。低于 min 的样本被丢弃并重新抽样	实数	N/A
max	最大粒径。高于 max 的样本被丢弃并重新抽样	实数	N/A
bins	用于离散化分布以近似初始条件区域内粒子数量的箱数	整数	64

在以下示例中，一个体积为 0.001 m³ 的长方体被填充为以数量加权的正态分布，平均直径为 1 mm，标准差为 0.25 mm。最小和最大粒径分别为 0.25 mm 和 1.75 mm。

列表 11 定义数量加权 normal 分布的输入片段。这不是完整的输入文件。

# 定义 IC 和 BC 的区域
# -----------------------------------------------------------------------
mfix.regions = full-domain

regions.full-domain.lo  = 0.0  0.0  0.0
regions.full-domain.hi  = 0.1  0.1  0.1

# 初始条件
# -----------------------------------------------------------------------
ic.regions = full-domain

mfix.particle_init_type = Auto

# 全域
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~>
ic.full-domain.fluid.volfrac  = 0.95

ic.full-domain.fluid.density  = 1.0
ic.full-domain.fluid.pressure = 0.0
ic.full-domain.fluid.velocity = 0.0  0.0  0.0

ic.full-domain.solids  = solid0

ic.full-domain.packing = random

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = normal
ic.full-domain.solid0.diameter.type = number-weighted
ic.full-domain.solid0.diameter.mean = 1000.e-6  # (m)
ic.full-domain.solid0.diameter.std  =  250.e-6  # (m)
ic.full-domain.solid0.diameter.min  =  250.e-6  # (m)
ic.full-domain.solid0.diameter.max  = 1750.e-6  # (m)

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  = 2500.0 # (kg/m^3)

使用这些设置的 MFIX-Exa DEM 模拟生成大约 81,700 个粒子。粒径分布如 图 9 所示（空心圆圈），此外还有数量加权（橙色）和体积加权（蓝色）密度函数。如 Weiner [Wei11] 所述，体积加权概率密度函数（PDF）相对于数量加权 PDF 向右偏移。

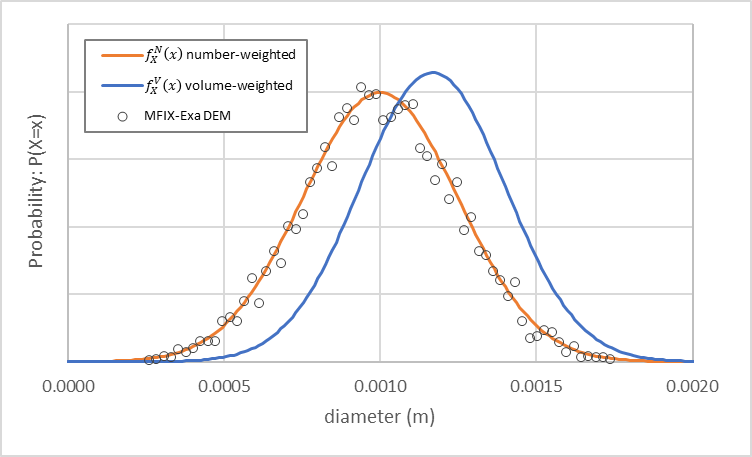
图 9 MFIX-Exa DEM 从示例输入生成的粒径分布（空心圆圈）。还绘制了具有 1 mm 均值和 0.25 mm 标准差的数量加权密度函数（橙色）和具有约 1.17 mm 均值和约 0.23 mm 标准差的体积加权密度函数（蓝色）。

在相同设置下，当 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 32 且欧拉网格间距 \(\Delta x\) 为 3.125 mm 时，MFIX-Exa PIC 模拟生成大约 82,000 个包裹。包裹尺寸分布如 图 10 所示（空心三角形），遵循体积加权密度函数。小闭合圆圈显示有效粒径分布，通过将每个观测值乘以包裹统计权重计算得出。例如，如果一个包裹的统计权重为 10，则在捕获包裹直径的箱中记录 10 次观测。

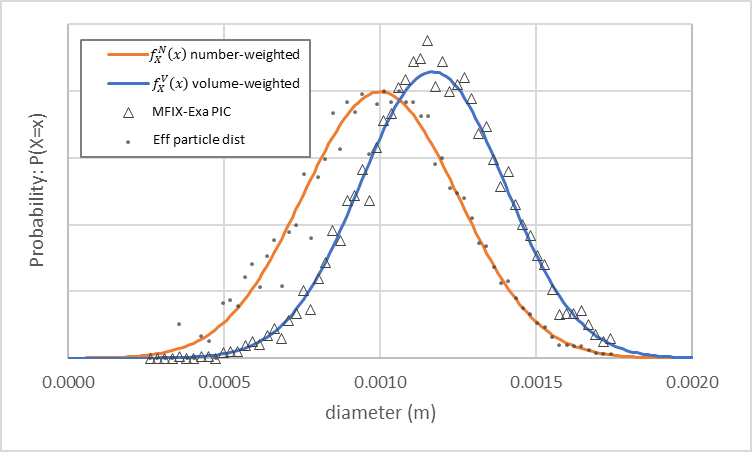
图 10 从示例输入生成的 MFIX-Exa PIC 包裹尺寸分布（空心三角形）。还绘制了具有 1 mm 均值和 0.25 mm 标准差的数量加权密度函数（橙色）和具有约 1.17 mm 均值和约 0.23 mm 标准差的体积加权密度函数（蓝色）。

以下部分概述了 MFIX-Exa 如何根据数量加权正态密度函数参数计算体积加权正态密度函数参数，以及如何根据体积加权密度函数参数计算数量加权正态密度函数参数。

从数量加权正态密度函数参数 \(\mu_N\) 和 \(\sigma_N\) 计算体积加权正态密度函数参数 \(\mu_V\) 和 \(\sigma_V\)

从正态分布的数量加权密度函数 \(f_X^N(x)\) 计算的体积加权密度函数 \(f_X^V(x)\) 是一个均值为 \(\mu_V\) 和方差为 \(\sigma_V^2\) 的正态分布。通过将 (1) 乘以 \(x^3\) 并代入数量加权分布的均值和标准差可得到体积加权密度函数的表达式。

\[\tilde{f}_X^V(x) = \frac{x^3}{\sigma_N \sqrt{2\pi}} \exp{\left(- \frac{(x - \mu_N)^2 }{ 2 \sigma_N^2 }\right)}\]

该分布的均值计算为

(2)\[\begin{split}\begin{align} \mu_V =& \frac{ \int_{-\infty}^{\infty} x \tilde{f}_X^V(x) dx }{\int_{-\infty}^{\infty} \tilde{f}_X^V(x) dx } \\[10pt] =& \frac{3\sigma_N^4 + 6\sigma_N^2\mu_N^2 + \mu_N^4}{3\sigma_N^2 \mu_N + \mu_N^3} \end{align}\end{split}\]

方差为

(3)\[\begin{split}\begin{align} \sigma^2_V =& \frac{ \int_{-\infty}^{\infty} (x - \mu_V)^2 \tilde{f}_X^V(x) dx }{\int_{-\infty}^{\infty} \tilde{f}_X^V(x) dx } \\[10pt] =& \frac{3\sigma_N^4 (3\mu_N + 2b) + \sigma^2(\mu_N^3 + 6\mu_N^2 b + 3\mu_Nb^2)+\mu_N^3 b^2}{3\sigma_N^2 \mu_N + \mu_N^3} \end{align}\end{split}\]

其中 \(b = (\mu_N - \mu_V)\)。由于体积加权分布是正态分布，计算出的均值和方差可以直接代入 (1)。

\[f_X^V(x) = \frac{1}{\sigma_V \sqrt{2\pi}} \exp{\left(- \frac{(x - \mu_V)^2 }{ 2 \sigma_V^2 }\right)}\]

从体积加权正态密度函数参数 \(\mu_V\) 和 \(\sigma_V\) 计算数量加权正态密度函数参数 \(\mu_N\) 和 \(\sigma_N\)

通过求解从 (2) 和 (3) 构建的非线性方程组来计算从体积加权均值和标准差 \(\mu_V\) 和 \(\sigma_V\) 得到的数量加权密度函数均值和标准差 \(\mu_N\) 和 \(\sigma_N\)。

\[\begin{split}\begin{align} f_1(\mu_N,\sigma_N) &= \left( 3\sigma_N^4 + 6\sigma_N^2\mu_N^2 + \mu_N^4 \right) - \mu_V \left( 3\sigma_N^2 \mu_N + \mu_N^3 \right) = 0 \\ f_2(\mu_N,\sigma_N) &= \left(3\sigma_N^4 (3\mu_N + 2b) + \sigma^2(\mu_N^3 + 6\mu_N^2 b + 3\mu_Nb^2)+\mu_N^3 b^2\right) - \sigma^2_V \left( 3\sigma_N^2 \mu_N + \mu_N^3 \right) = 0 \end{align}\end{split}\]

使用 Burden and Faires [BF10] 中概述的同伦法求解该系统。为了确保快速收敛，初始猜测 \(\mu_N\) 和 \(\sigma_N\) 是通过将 (1) 除以 \(x^3\) 并代入体积加权分布的均值和标准差 \(\mu_V\) 和 \(\sigma_V\) 创建的密度函数计算的。

(4)\[\tilde{f}_X^N(x) = \frac{1}{x^3\sigma_V \sqrt{2\pi}} \exp{\left(- \frac{(x - \mu_V)^2 }{ 2 \sigma_V^2 }\right)}\]

\(\tilde{f}_X^N(x)\) 如 图 11 所示，不是数量加权密度函数，而是对它的近似。均值和方差通过对 \(x \in \left[ x_\mathrm{min}, x_\mathrm{max} \right]\) 区间内的 \(\tilde{f}_X^N(x)\) 进行数值积分计算，其中 \(x_{min}\) 和 \(x_{mid}\) 通过将 (4) 的导数设为零并计算根得出。\(x_\mathrm{max}\) 选择为在中点镜像 \(x_\mathrm{min}\)。

(5)\[\begin{split}\begin{align} x_{\mathrm{min}} \; =& \; \left( \mu_V - \sqrt{\mu_V^2 -12\sigma_V^2}\right)/2 \\ x_{\mathrm{mid}} \; =& \; \left(\mu_V + \sqrt{\mu_V^2 -12\sigma_V^2}\right)/2 \\ x_{\mathrm{max}} \; =& \; 2x_{\mathrm{mid}} - x_{\mathrm{min}} \end{align}\end{split}\]

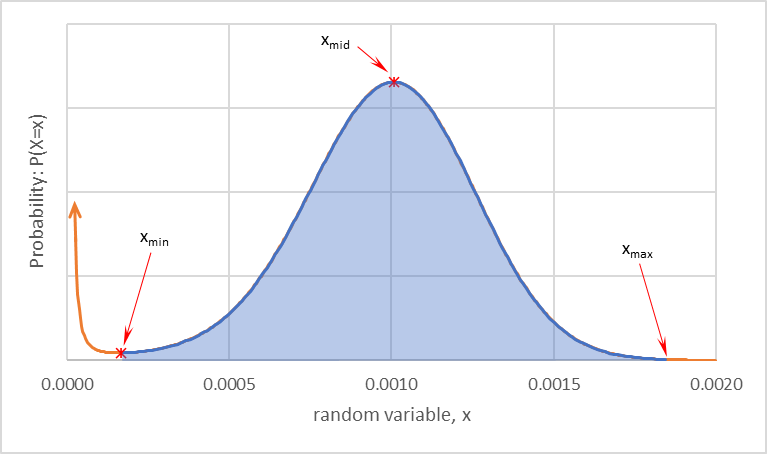
图 11 通过将体积加权分布函数除以 x³ 近似的数量加权正态分布函数。通过从 x_min 到 x_max 数值积分计算近似均值和方差。

采样正态分布

MFIX-Exa 采样均值为 m_mean 和标准差为 m_stddev 的正态分布以返回分布观测值。

amrex::Real observation;

do { observation = amrex::RandomNormal(m_mean, m_stddev, a_engine); }
while (!(m_min <= observation && observation <= m_max));

return observation;

函数 amrex::RandomNormal 返回一个伪随机实数（双精度）。样本被丢弃并再次对分布进行采样，直到值满足 \(\mathrm{xmin} \le x\) 和 \(x \le \mathrm{xmax}\)。

log-normal 分布

log-normal 分布由以下公式给出

\[f_X(x) = \frac{d}{dx}F_X(x) = \frac{1}{x \sigma \sqrt{2\pi}} \exp{\left(- \frac{(\mathrm{ln}(x) - \mu)^2 }{ 2 \sigma^2 }\right)}\]

其中 \(\mu\) 和 \(\sigma\) 是定义分布的参数。

备注

\(\mu\) 和 \(\sigma\) 不是 \(x\) 的均值和标准差。它们是 \(\mathrm{ln}(x)\) 的均值和标准差。对数正态随机变量的均值（期望）:math:E(x) 和方差 \(V(x)\) 给出如下

\[E(x) = \exp{\left(\mu + \sigma^2/2\right)}\]

和

\[V(x) = \exp{\left(2\mu + 2\sigma^2\right)} - \exp{\left(2\mu + \sigma^2\right)}\]

分别见 Navidi [Nav14] 了解对数正态分布的概述。

	描述	类型	默认值
type	分布加权类型： number-weighted 或 volume-weighted	字符串	N/A
mean	正态随机变量的均值, \(\mathrm{ln}(X)\)	实数	N/A
stddev	正态随机变量的标准差, \(\mathrm{ln}(X)\)	实数	N/A
min	最小粒径。低于 min 的样本将被丢弃并重新抽样。	实数	N/A
max	最大粒径。超过 max 的样本将被丢弃并重新抽样。	实数	N/A
bins	离散化分布时使用的箱数，以近似初始条件区域内的颗粒数量。	整数	64

在以下示例中，一个体积为 0.001 m³ 的长方体被填充为具有列出参数的体积加权对数正态分布。最小和最大粒径分别为 0.23 mm 和 3.00 mm。

列表 12 定义数加权 log-normal 分布的输入片段。这不是完整的输入文件。

# 定义 IC 和 BC 的区域
# -----------------------------------------------------------------------
mfix.regions = full-domain

regions.full-domain.lo  = 0.0  0.0  0.0
regions.full-domain.hi  = 0.1  0.1  0.1

# 初始条件
# -----------------------------------------------------------------------
ic.regions = full-domain

mfix.particle_init_type = Auto

# 全域
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~>
ic.full-domain.fluid.volfrac  = 0.75

ic.full-domain.fluid.density  = 1.0
ic.full-domain.fluid.pressure = 0.0
ic.full-domain.fluid.velocity = 0.0  0.0  0.0

ic.full-domain.solids  = solid0

ic.full-domain.packing = random

ic.full-domain.solid0.volfrac   = 0.25
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = log-normal
ic.full-domain.solid0.diameter.type = volume-weighted
ic.full-domain.solid0.diameter.mean = -3.662955279
ic.full-domain.solid0.diameter.std  =  1.04
ic.full-domain.solid0.diameter.min  =   30.e-6  # (m)
ic.full-domain.solid0.diameter.max  = 3000.e-6  # (m)

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  = 2500.0 # (kg/m^3)

使用这些设置的 MFIX-Exa DEM 仿真生成约 162,000 个颗粒。颗粒大小分布（空心圆）、数加权（橙色）和体积加权（蓝色）密度函数如 图 12 所示。

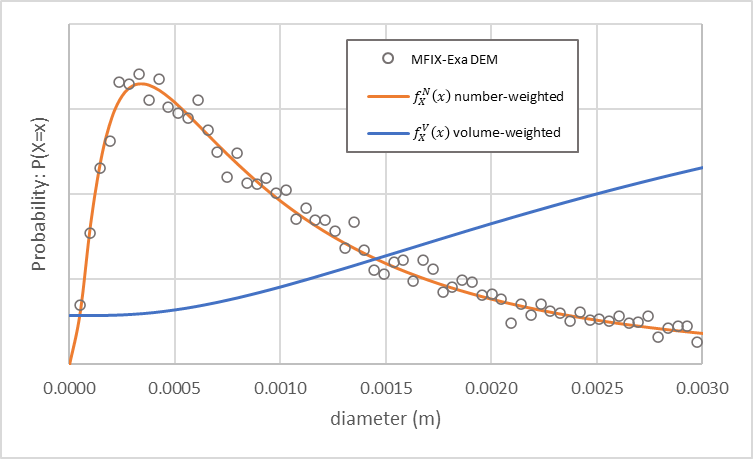
图 12 MFIX-Exa DEM 颗粒大小分布（空心圆）和数加权（橙色）和体积加权（蓝色）密度函数。

使用相同设置的 MFIX-Exa PIC 仿真在 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 32 和欧拉网格间距 \(\Delta x\) 为 3.125 mm 时生成约 410,000 个包裹。 图 13 显示了包裹大小分布（空心三角形）和数加权（橙色）和体积加权（蓝色）密度函数。同样，小闭合圆表示由 PIC 包裹捕获的有效颗粒分布。

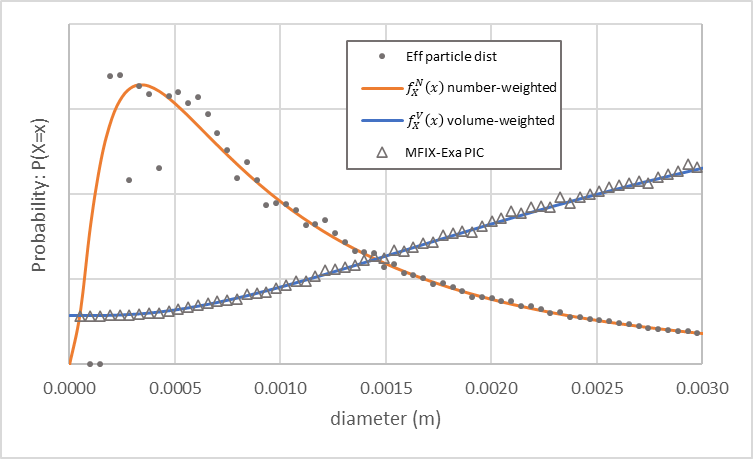
图 13 MFIX-Exa PIC 包裹大小分布（空心三角形）、数加权密度函数（橙色）和体积加权密度函数（蓝色）。小闭合圆表示由包裹建模的颗粒大小分布。

在对数正态分布之间转换数加权和体积加权参数

如 El-Hilo [EH12], El-Hilo and Chantrell [EHC12] 所述，数加权和体积加权对数正态分布使用相同的 \(\sigma\) 参数

\[\sigma = \sigma_{N} = \sigma_{V}\]

而参数 \(\mu\) 是直接从其他分布计算的。

\[\begin{split}\begin{align} \mu_V =& \mu_N + 3.0\sigma^2 \\[10pt] \mu_N =& \mu_V - 3.0\sigma^2 \end{align}\end{split}\]

采样对数正态分布

MFIX-Exa 不是采样对数正态分布，而是采样均值为 m_mean 和标准差为 m_stddev 的正态分布。

amrex::Real observation;

do { observation = amrex::RandomNormal(m_mean, m_stddev, a_engine); }
while (!(m_log_min <= observation && observation <= m_log_max));

return std::exp(observation);

函数 amrex::RandomNormal 返回一个伪随机实数（双精度）。样本被丢弃，分布重新采样，直到值满足 \(\log \mathrm{xmin} \le \log x\) 和 \(\log x \le \log \mathrm{xmax}\)。通过应用指数函数返回对数正态变量 \(x = \exp ( \log x )\)。

uniform 分布

uniform 分布由以下公式给出

(6)\[\begin{split}f_X(x) = \frac{d}{dx}F_X(x) = \begin{cases} \left(x_\mathrm{max} - x_\mathrm{min}\right)^{-1}, & \text{当} \; x \in \left[ x_\mathrm{min}, x_\mathrm{max} \right] \\ 0, & \text{否则} \end{cases}\end{split}\]

其中 \(x_\mathrm{min}\) 和 \(x_\mathrm{max}\) 是最小和最大粒子直径。用于指定分布的输入在下表中提供。

	描述	类型	默认值
type	分布加权方式： number-weighted 或 volume-weighted	字符串	N/A
min	最小粒子直径。低于 min 的样本被丢弃并重新抽样	实数	N/A
max	最大粒子直径。高于 max 的样本被丢弃并重新抽样	实数	N/A
bins	离散化分布时使用的箱数，用于近似初始条件区域内的粒子数	整数	64

在以下示例中，一个体积为 0.001 m³ 的长方体被填充为数权均匀分布。最小和最大粒子直径分别为 0.25 mm 和 1.75 mm。

列表 13 定义数权 uniform 分布的输入片段。这不是完整的输入文件。

# 定义 ICs 和 BCs 的区域
# -----------------------------------------------------------------------
mfix.regions = full-domain

regions.full-domain.lo  = 0.0  0.0  0.0
regions.full-domain.hi  = 0.1  0.1  0.1

# 初始条件
# -----------------------------------------------------------------------
ic.regions = full-domain

mfix.particle_init_type = Auto

# 全域
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~>
ic.full-domain.fluid.volfrac  = 0.95

ic.full-domain.fluid.density  = 1.0
ic.full-domain.fluid.pressure = 0.0
ic.full-domain.fluid.velocity = 0.0  0.0  0.0

ic.full-domain.solids  = solid0

ic.full-domain.packing = random

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = uniform
ic.full-domain.solid0.diameter.type = number-weighted
ic.full-domain.solid0.diameter.min  =  250.e-6  # (m)
ic.full-domain.solid0.diameter.max  = 1750.e-6  # (m)

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  = 2500.0 # (kg/m^3)

使用这些设置的 MFIX-Exa DEM 仿真生成大约 110,000 个粒子。粒子大小分布（空心圆），数权（橙色）和体积权（蓝色）密度函数如 图 14 所示。

图 14 MFIX-Exa DEM 均匀粒子大小分布（空心圆）和数权（橙色）及体积权（蓝色）均匀密度函数。

当 pic.close_pack = 0.64 和 pic.parcels_per_cell_at_pack = 32 ，以及欧拉网格间距 \(\Delta x\) 为 3.125 mm 时，具有相同设置的 MFIX-Exa PIC 仿真生成约 410,000 个包裹。图 15 显示了包裹大小分布（空心三角形）和数权（橙色）及体积权（蓝色）密度函数。同样，小实心圆表示由 PIC 包裹捕获的有效粒子分布。

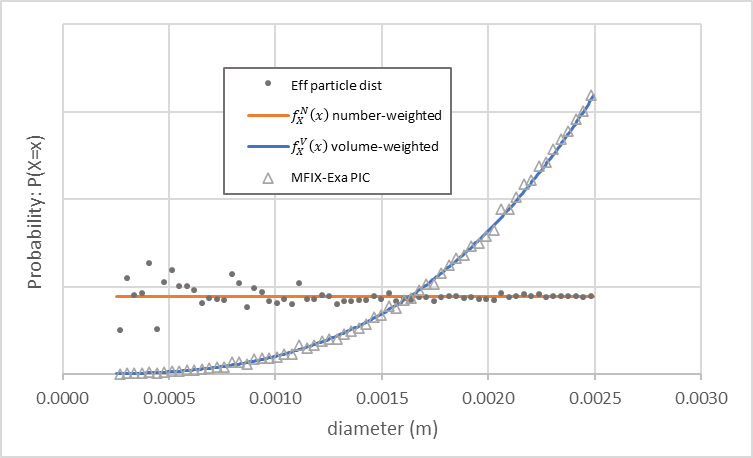
图 15 MFIX-Exa PIC 均匀包裹大小分布（空心三角形）、数权（橙色）和体积权（蓝色）均匀密度函数。小实心圆表示包裹模拟的粒子大小分布。

采样均匀分布

在指定数权分布的 DEM 仿真和指定体积权分布的 PIC 仿真中，计算一个均匀分布的变量 \(rand \in \left( 0, 1 \right)\)，然后对结果进行缩放和平移，使得 \(x \in \left[ x_\mathrm{min}, x_\mathrm{max} \right)\)。

amrex::Real rand = amrex::Random(a_engine);

return m_min + (m_max-m_min)*rand;

函数 amrex::Random 返回一个从 0.0 到 1.0（包含 0.0，不包含 1.0）均匀分布的伪随机实数（双精度）。

当为 DEM 仿真指定体积权分布和为 PIC 仿真指定数权分布时，使用逆采样。这种方法使用逆函数 \(F^{-1}\) 从连续分布函数 \(F\) 生成随机变量。

如果 \(\mathcal{U}\) 是区间 \([0,1]\) 上的均匀随机变量，并且 \(F\) 是区间 \([a,b]\) 上的连续累积分布函数，具有逆函数

\[F^{-1}(u) = \inf \left\{ x: F(x) = u \right\}\]

则 \(F^{-1}(\mathcal{U})\) 具有累积分布函数 \(F\) （改编自 Devroye [Dev86]）。

数权密度函数 \(f_X^N(x)\) 是通过将 (6) 除以 \(x^3\) 从指定的体积权密度函数计算出来的。出于简洁目的，指示密度函数在 \(x \notin \left[ x_\mathrm{min}, x_\mathrm{max} \right]\) 时为零的括号符号被省略。

\[f_X^N(x) = \frac{1}{x^3 (x_{\mathrm{min}} - x_{\mathrm{max}})}\]

累积分布函数及其逆函数是

\[\mathrm{Pr}\left(X \le x\right) = F_X^N(x) = \frac{ \int_{a}^{x} f_X^N(y) dy }{\int_{a}^{b} f_X^N(y) dy } = \frac{ b^2(x^2-a^2)}{x^2(b^2 - a^2)}\]

和

\[{F_X^N}^{-1}(u) = \frac{ab}{\sqrt{b^2 - u(b^2 -a^2)}}\]

其中 \(a = x_{\mathrm{min}}\) 和 \(b = x_{\mathrm{max}}\)。要采样 \(f_X^V(x)\)，生成一个均匀分布的变量 \(u \in \mathcal{U}(0,1)\) 并代入逆累积分布函数。

amrex::Real rand = amrex::Random(a_engine);

amrex::Real const b(m_max);
amrex::Real const a(m_min);

amrex::Real const a2(a*a), b2(b*b);

return (a*b)/std::sqrt(b2 - rand*(b2-a2));

类似地，体积权密度函数 \(f_X^V(x)\) 是通过将 (6) 乘以 \(x^3\) 从数权分布计算出来的。出于简洁目的，指示密度函数在 \(x \notin \left[ x_\mathrm{min}, x_\mathrm{max} \right]\) 时为零的括号符号被省略。

\[f_X^V(x) = \frac{x^3}{(x_{\mathrm{min}} - x_{\mathrm{max}})}\]

累积分布函数及其逆函数是

\[\mathrm{Pr}\left(X \le x\right) = F_X^V(x) = \frac{ \int_{a}^{x} f_X^V(y) dy }{\int_{a}^{b} f_X^V(y) dy } = \frac{ x^4 - a^4 }{ b^4 - a^4 }\]

和

\[{F_X^V}^{-1}(u) = \left(a^4 + u(b^4 - a^4)\right)^{1/4}\]

其中 \(a = x_{\mathrm{min}}\) 和 \(b = x_{\mathrm{max}}\)。要采样 \(f_X^V(x)\)，生成一个均匀分布的变量 \(u \in \mathcal{U}(0,1)\) 并代入逆累积分布函数。

amrex::Real rand = amrex::Random(a_engine);

amrex::Real const b(m_max);
amrex::Real const a(m_min);

amrex::Real const a4(a*a*a*a), b4(b*b*b*b);

return std::pow(a4 + rand*(b4-a4),0.25);

custom 分布

用户自定义的 custom 分布可以通过文本文件提供离散概率来指定。

	描述	类型	默认值
custom	用户定义分布的文件名	字符串	N/A
min	最小粒径。低于 min 的样本将被丢弃并重新抽样	实数	N/A
max	最大粒径。高于 max 的样本将被丢弃并重新抽样	实数	N/A
interpolate	启用离散区间之间的线性插值。此选项仅在初始分布概率为零时可用。	布尔值	false

分布输入文件包含四个部分：

• 第1行：分布条目数（整数）

• 第2行：指定分布为 CDF 或 PDF （字符串）

• 第3行：注释或空行（求解器未使用）

• 剩余行定义区间和概率（实数 实数）

以下部分提供了一些自定义分布配置的示例。

无插值的双分散混合物

在以下示例中，体积为 0.001 m³ 的长方体中填充了一个按数量加权的分布。 该分布是两种粒径的 50/50 混合物。

列表 14 定义按数量加权的 custom 分布的输入片段。这不是完整的输入文件。

# 定义 IC 和 BC 的区域
# -----------------------------------------------------------------------
mfix.regions = full-domain

regions.full-domain.lo  = 0.0  0.0  0.0
regions.full-domain.hi  = 0.1  0.1  0.1

# 初始条件
# -----------------------------------------------------------------------
ic.regions = full-domain

mfix.particle_init_type = Auto

# 全域
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~>
ic.full-domain.fluid.volfrac  = 0.95

ic.full-domain.fluid.density  = 1.0
ic.full-domain.fluid.pressure = 0.0
ic.full-domain.fluid.velocity = 0.0  0.0  0.0

ic.full-domain.solids  = solid0

ic.full-domain.packing = random

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = custom
ic.full-domain.solid0.diameter.custom = bidisperse-pdf.dist
ic.full-domain.solid0.diameter.type = number-weighted

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  =  2500.0    # (kg/m^3)

ic.full-domain.solid0.density =  constant
ic.full-domain.solid0.density.constant  = 2500.0 # (kg/m^3)

列表 15 定义两种粒径50/50混合的自定义分布。

2
PDF
# 双分散混合物
 500.e-6  0.5
1000.e-6  0.5

使用这些设置的 MFIX-Exa DEM 模拟生成大约 180,000 个粒子，其中一半的粒子直径为 0.5 mm，另一半为 1.0 mm。 相同设置下的 MFIX-Exa PIC 模拟在 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 32 和欧拉网格间距 \(\Delta x\) 为 3.125 mm 时生成大约 82,000 个包裹。大约 10% 的包裹直径为 0.5 mm，90% 为 1.0 mm。

双峰混合物

以下示例使用与前一个示例相同的布局，但自定义分布为 CDF，描述了通过组合两个正态分布创建的双峰分布。

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = custom
ic.full-domain.solid0.diameter.custom = bimodal-cdf.dist
ic.full-domain.solid0.diameter.type = number-weighted

列表 16 通过组合两个正态分布创建的自定义双峰分布

25
CDF
# 由两个正态分布创建的双峰分布
0.000144  0.0000
0.000240  0.0063
0.000336  0.0360
0.000384  0.0818
0.000416  0.1356
0.000432  0.1919
0.000456  0.2495
0.000480  0.3053
0.000496  0.3587
0.000528  0.4055
0.000568  0.4447
0.000584  0.4822
0.000600  0.5191
0.000616  0.5566
0.000632  0.5958
0.000664  0.6408
0.000704  0.6942
0.000720  0.7501
0.000752  0.8075
0.000768  0.8638
0.000784  0.9177
0.000816  0.9635
0.000864  0.9932
0.000960  0.9995
0.001056  1.0000

使用这些设置的 MFIX-Exa DEM 模拟生成大约 2,285,000 个粒子。粒径分布（空心圆圈）、数量加权（橙色）、和体积加权（蓝色）密度函数如 图 16 所示。

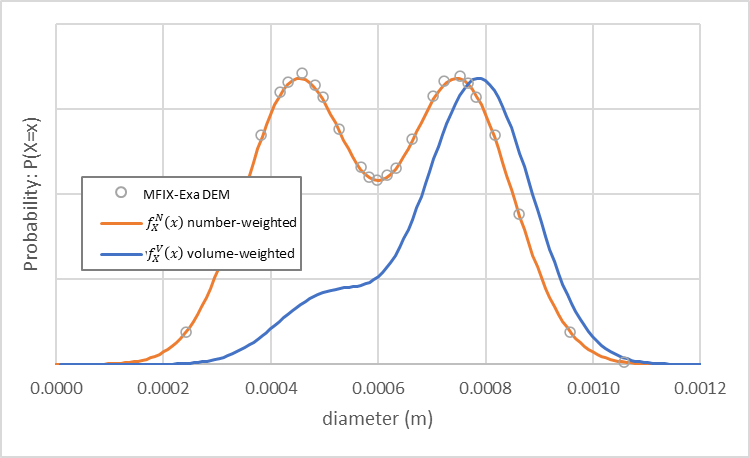
图 16 MFIX-Exa DEM 自定义双峰粒径分布（空心圆圈）以及数量加权（橙色） 和体积加权（蓝色）密度函数。

相同设置下的 MFIX-Exa PIC 模拟在 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 32 和欧拉网格间距 \(\Delta x\) 为 3.125 mm 时生成大约 82,000 个包裹。包裹尺寸分布如 图 17 所示（空心三角形）遵循体积加权密度函数。小闭合圆圈表示通过将每个观测值乘以包裹统计权重计算的有效粒径分布。

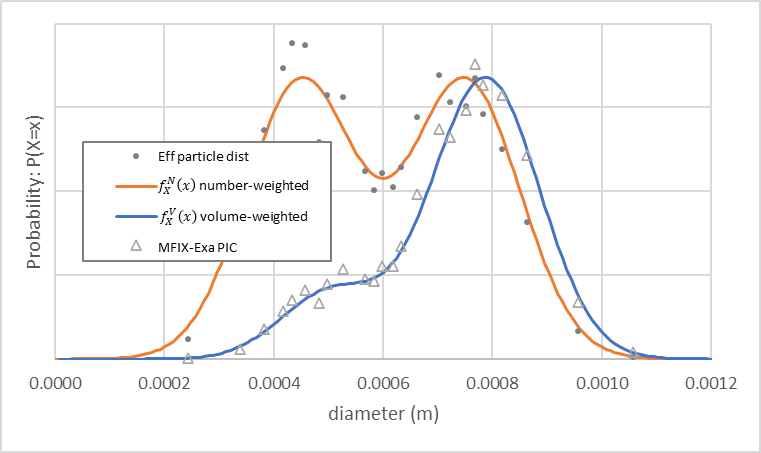
图 17 MFIX-Exa PIC 自定义双峰包裹尺寸分布（空心三角形）、数量加权（橙色）和 体积加权（蓝色）密度函数。小闭合圆圈表示包裹模拟的粒径分布。

测量的尺寸分布

最后一个示例使用与前面示例相同的布局，但自定义分布为描述实验测量的尺寸分布的 CDF，分布类型为 volume-weighted 。

ic.full-domain.solid0.volfrac   = 0.05
ic.full-domain.solid0.velocity  = 0.00  0.00  0.00

ic.full-domain.solid0.diameter = custom
ic.full-domain.solid0.diameter.custom = qicpic-cdf.dist
ic.full-domain.solid0.diameter.type = volume-weighted

列表 17 测量的自定义分布

32
CDF

0.00025   0.0013499
0.000298387   0.00250452
0.000346774   0.00448884
0.000395161   0.00777403
0.000443548   0.0130136
0.000491935   0.0210638
0.000540323   0.0329789
0.00058871   0.0499683
0.000637097   0.0733046
0.000685484   0.104184
0.000733871   0.143547
0.000782258   0.191886
0.000830645   0.24907
0.000879032   0.314239
0.000927419   0.385785
0.000975806   0.461453
0.00102419   0.538547
0.00107258   0.614215
0.00112097   0.685761
0.00116935   0.75093
0.00121774   0.808114
0.00126613   0.856453
0.00131452   0.895816
0.0013629   0.926695
0.00141129   0.950032
0.00145968   0.967021
0.00150806   0.978936
0.00155645   0.986986
0.00160484   0.992226
0.00165323   0.995511
0.00170161   0.997495
0.00175   0.99865

使用这些设置的 MFIX-Exa DEM 模拟生成大约 963,000 个粒子。粒径分布（空心圆圈）、数量加权（橙色加号）、和体积加权（蓝色叉号）概率如 图 18 所示。

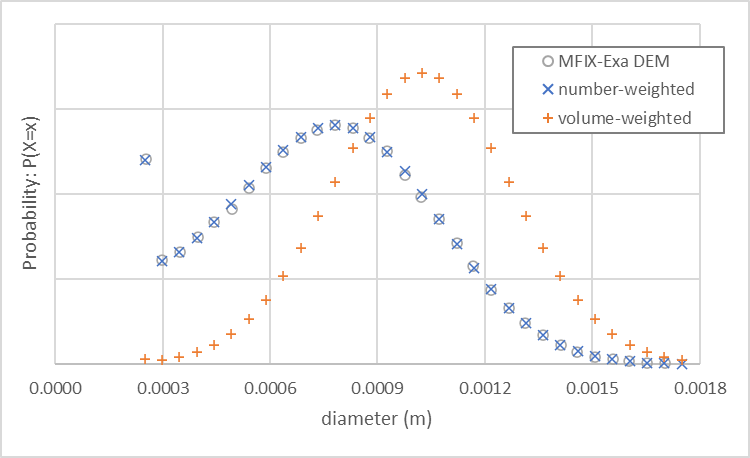
图 18 MFIX-Exa DEM 自定义双峰粒径分布（空心圆圈）以及数量加权（橙色加号） 和体积加权（蓝色叉号）概率。

相同设置下的 MFIX-Exa PIC 模拟在 pic.close_pack = 0.64 、 pic.parcels_per_cell_at_pack = 64 和欧拉网格间距 \(\Delta x\) 为 3.125 mm 时生成大约 164,000 个包裹。包裹尺寸分布如 图 19 所示（空心三角形）遵循体积加权概率。小闭合圆圈表示通过将每个观测值乘以包裹统计权重计算的有效粒径分布。

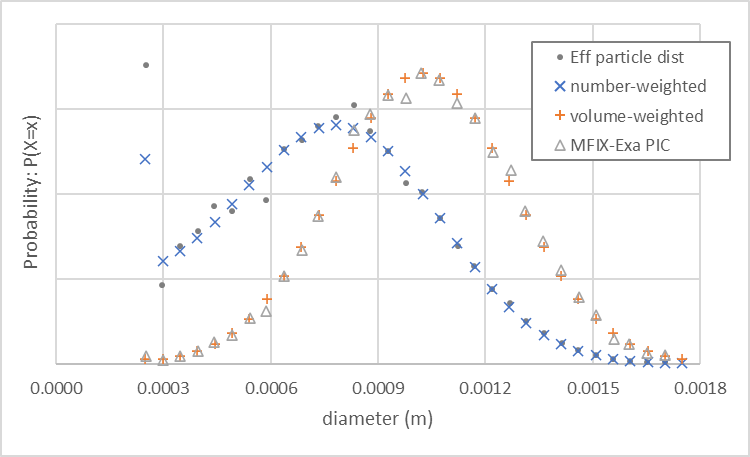
图 19 MFIX-Exa PIC 自定义双峰包裹尺寸分布（空心三角形）、数量加权（橙色加号） 和体积加权（蓝色叉号）概率。小闭合圆圈表示包裹模拟的粒径分布。