颗粒瑞利-泰勒不稳定性
瑞利-泰勒 (RT) 不稳定性与开尔文-亥姆霍兹不稳定性一起,是所有多相流不稳定性中最著名和最基础的 [C81] 。原型案例涉及两种(传统)流体处于静止状态,密度不同,较重的流体被加速进入较轻的流体。不稳定性表现为两个流体之间界面的变形。初始变形发展为一种相互渗透的指状图案,通常会产生蘑菇云图案,随后在流体不混溶的情况下,转变为微观尺度的混合或气泡-液滴形成。
Vinningland 和同事 [VJFTM07] 设计了一个经典问题的颗粒模拟,其中较重的“流体”是一组粒子渗透到气体中,在这种情况下为空气。粒子组通过在重力作用下在 Hele-Shaw 细胞(矩形封闭空间)中沉降并形成随机紧密堆积阵列来生成,然后迅速围绕一个枢轴旋转,使较重的粒子相位位于较轻的气相上方。不稳定性的演变与经典的流体-流体 RT 不同,正如 Vinningland 等人所描述的 [VJFTM07] :
起初由颗粒定义的平坦前端随后发展成下落的颗粒指状图案,指状图案之间是上升的空气泡。起初通过指状合并过程观察到前端的短暂粗化。粗化随后通过从上升气泡中心生长的新指状得以稳定。
使用 MFIX-Exa 19.08 模拟颗粒 RT,设置如下。域宽 56 mm,高 68 mm,深 1 mm,通过一个均匀网格离散化为 \(224 \times 272 \times 4\) 个 CFD 单元。在域的顶部、底部、左侧和右侧应用无滑移壁面。前后墙在模拟中被“移除”并被视为周期性,因为深度仅由四个 CFD 单元解析。
无需其他几何定义。
假设粒子是单分散的,直径恒定为 \(d_p = 140\) 微米 (\(dx^* \approx 1.8\)),密度为 \(\rho_p = 1050\) kg/m3 。恢复和滑动摩擦系数设置为 0.9 和 0.25,认为代表了聚苯乙烯材料。应用 Wen 和 Yu 的 WenYu 阻力定律 [WY66] 。最初在整个域中随机分布 1.12M 粒子。粒子的重力通过 \(\tanh 100(t - 2)\) 被修改,使得粒子最初向上沉降,然后在 \(t = 2\) 秒左右迅速反转体力,导致粒子向下落入静止的空气中。
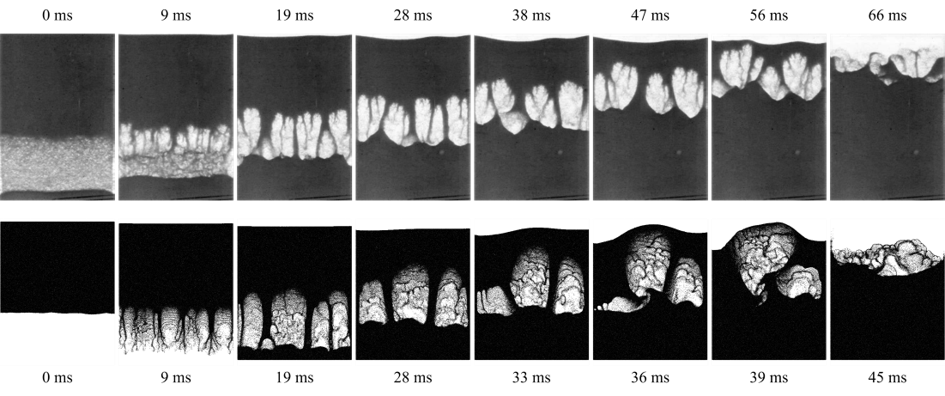
图 22 Vinningland 等人的颗粒瑞利-泰勒不稳定性实验 [VJFTM07] (上排)与 MFIX-Exa 结果(下排)的进展对比。
上图显示了 MFIX-Exa 19.08 模拟与实验结果的进展对比。实验和数值结果在瞬态的前半部分大致吻合:最初的平坦界面让位于许多掉入气体中的指状,这些指状合并形成一个半稳定的气泡图案。然而,模拟的气泡似乎比实验室中的气泡更不稳定,实验室中的气泡均匀上升至表面。然而,在模拟中,中心气泡上升速度稍快于左侧气泡,这将更多的重量转移到左侧气泡,从而进一步阻碍其上升,最终在突破表面时将左侧气泡“挤压”到中心气泡中。稍后,右侧气泡也与(剩下的)中心气泡合并,允许其空气找到一条最小阻力的路径逃逸,而不会自行破裂于表面。气泡合并显著加速了瞬态的后半部分(注意实验和模拟之间的不同时间)。进行了该设置的几种不同变体:不同的阻力定律、较慢的反转时间、不同的粒子恢复和摩擦系数组合、包含前后墙。尽管所有测试略有不同,但没有一个能够匹配实验中观察到的后期气泡图案的稳定性。