HCS 中的聚集

HCS 是最简单的非平凡颗粒气-固系统。连续气相最初处于静止状态。颗粒均匀地分布在空间中，并且在所有三个方向上的动量为零。然而，颗粒的特殊速度不为零，由初始 颗粒 温度 \(T_0\) 量化。系统在所有方向上都是周期性的，没有外力作用于系统。在均匀条件下，颗粒温度 \(T\) 相当于 (无质量的) 平均颗粒动能的三分之二。在 HCS 中，Garzo 等人的欧拉动力学理论 (KT) 模型 [GTSH12] 简化为：

\[\frac{dT}{dt} = - \frac{2 \gamma}{m} T - \zeta_0 T\]

其中 \(m\) 是颗粒质量，\(\gamma\) 是热拖曳，\(\zeta_0\) 是零阶冷却速率。上面右侧的第一项表示由于间隙气体引起的粘性耗散，而第二项表示由于非弹性颗粒间相互作用引起的碰撞耗散。该常微分方程有一个由 Yin 等人提供的解析解 [YZMH13] （另见 [LBFHHGS16] 获取此处使用的精确模型，该模型还包括对 \(\gamma\) 的一阶热雷诺数扩展）。在没有聚集的情况下，HCS 中的颗粒温度根据解析解衰减，称为颗粒系统中的 Haff 定律 [H83] ：\(\gamma = 0\)。然而，在一个临界系统尺寸 [G05] ， \(L^*_c\) ，(其中 \(L^* = L/d_p\) )，最初的均匀状态让位于气-固系统中最基本的不稳定性，即聚集不稳定性，这导致 \(T\) （或更准确地说 \(KE\) ）由于高浓度和低浓度区域以及相关运动显著偏离 KT 解。

为了测试 MFIX-Exa 是否预测到预期的聚集行为，建立了具有以下无量纲参数的系统：

  • 初始热雷诺数：\(Re_{T_0} = \rho_g d_p \sqrt{T_0} / \mu_g = 20\)

  • 密度比：\(\rho^* = \rho_p / \rho_g = 1000\)

  • 恢复系数：\(e = 0.8\)

  • 固体浓度：\(\phi = \pi N_p / 6 L^*_x L^*_y L^*_z \approx 0.05\)

虽然 Fullmer 等人没有特别研究过 [FLYH18] ，但他们的结果表明在这些条件下 \(L_c^*\) 可能高达 100。为了避免接近临界稳定性的区域，我们使用一个显著更大的系统尺寸：\(L^*_x = L^*_y = 256\)。系统在深度方向很薄，\(L^*_z = 8\) 以突出聚集现象。因此，\(N_p = 50000\)。由于系统是理论上的，应用了理想的 BVK2 DNS 拖曳定律，见 [BvK07] ，[TPKKv15] 。

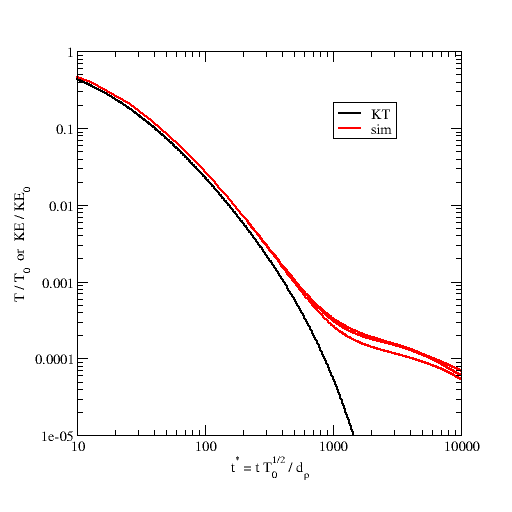
HCS 中的动能衰减

图 20 与 GTSH 模型的 KT 解析解相比的颗粒平均动能衰减。

使用 MFIX-Exa 19.08 模拟三个重复系统，唯一不同的是初始颗粒位置和特殊速度。在模拟中平均颗粒动能（红色）并与 HCS 的解析颗粒温度（黑色）作为时间函数进行比较，如上图所示。动能 \(KE / KE_0\) 按 HCS 结果衰减 2 到 3 个数量级，直到聚集和局部平均运动导致剧烈偏离。在 \(t^* = 1000\) 时，一个重复系统的最终结果如下所示（右侧），与 Goldhirsch 和 Zanetti 的开创性结果 [GZ93] （真正的 2D）相比，这是 HCS 中聚集不稳定性的最初示例。

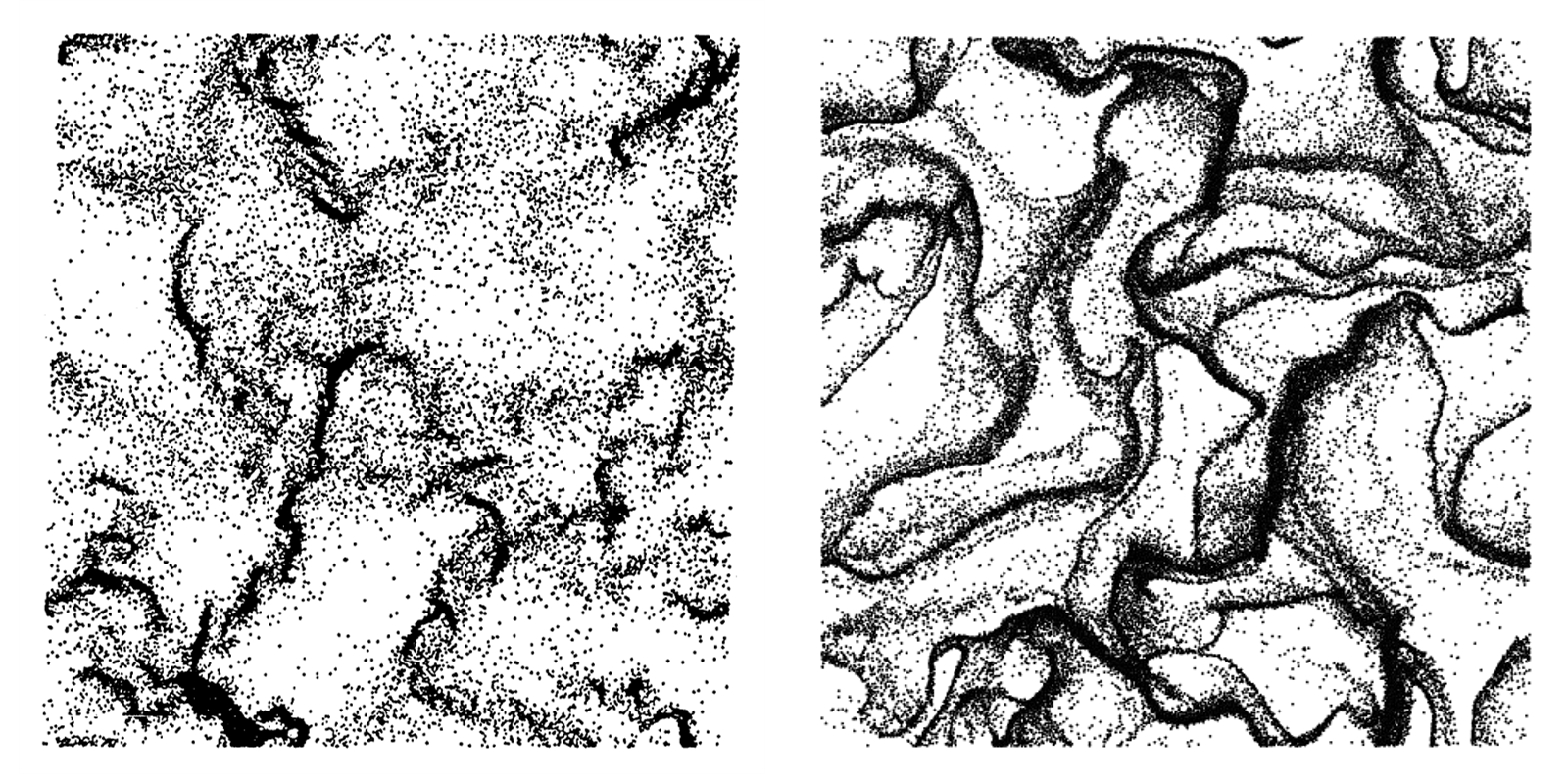
HCS 的聚集状态

图 21 Goldhirsch 和 Zanetti [GZ93] 观察到的 HCS 聚集状态（左）与 MFIX-Exa 结果（右）相比。